Un
format flexibil in virgula mobila pentru optimizarea
Data-Path-urilor si a
operatorilor in FPGA-urile bazate pe DSP-uri
REZUMAT
Procesarea semnalelor
video necesita algoritmi complecsi capabili sa faca
fata numeroaselor operatii de baza pe un dispozitiv video. Pentru a realiza
aceste calcule in timp real in cadrul unui FPGA, trebuie sa
utilizam structuri inovative capabile de obtinerea cerintelor de viteza
necesare. Ca parte a proiectului ce tine de
optimizarea unui dispozitiv de reducere a zgomotului unui semnal video s-a
creat un dispozitiv optimizat de procesare ce necesita cateva calcule in
virgula mobila. Aceasta documentatie prezinta principiul de
functionare a unitatii in virgula mobila, explica tipul de date reprezentate,
implementarea lor intr-un VirtexE FPGA Xilinx si raporteaza performantele
obtinute. Un divizor ce utilizeaza
reprezentarea este de asemenea prezent inclusiv cu implementarea sa si
performantele obtinute in cadrul aceluiasi FPGA.
1.INTRODUCERE
In
televiziunea de inalta definitie (HDTV), marimea imaginilor si cantitatea de
informatii in cadrul unui semnal video sunt foarte importante. HDTV
necesita o scurgere de informatii de 600Mbit/s dupa decompresie. Imaginile HDTV sunt concepute pentru a fi de o calitate foarte
ridicata, dar exista cateva necesitati stricte referitor la compresia datelor
pentru o stocare mai eficienta si pentru limitarea necesitatilor referitoare la
latimea de banda. Astfel este nevoie de metode
care sa micsoreze impactul operatiilor de compresie/decompresie. Algoritmii optimi pentru aceasta cerinta sunt disponibili dar ei
solicita resurse foarte puternice ale procesarii. Algoritmul studiat
necesita peste 300 de operatii matematice si logice pentru fiecare pixel, ceea ce se traduce prin aproximativ 20 Giga de operatii
pe secunda. Asta este departe de capacitatile
existentelor DSP-uri, iar obtinerea performatelor in timp real fixeaza
cerintele pentru implementarea hardware. Cand astfel de algoritmi urmeaza a fi
implementati in FPGA-uri, trebuie sa tinem cont de 2
aspecte:
a)
complexitatea hardware (numarul de componente dintr-un
Virtex FPGA Xilinx si dimensiunea memoriilor incluse)
b)
timpul de procesare
pentru aplicatiile in timp real. Acesta devine o constrangere grea daca FPGA-
ul selectat intampina
dificultati in ceea ce priveste obtinerea cerintelor (de exemplu 75MHz)
Complexitatea
algoritmilor necesita aritmetica de inalta precizie (pe 20biti sau mai mult). La o precizie
ridicata, operatorii sunt complecsi si lenti ceea ce
determina o cresterea a cerintelor. O solutie pentru controlul complexitatii este utilizarea reprezentarii in virgula mobila atunci cand
este cazul. Necesitatea bazata pe majoritatea simularilor ne lasa pe noi sa stabilim unitatile de virgula mobila ca o necesitate
pentru controlul complexitatii hardware. Restul rapoartelor
scrise se refera la configurarea unitatii in virgula mobila implementata in
FPGA-urile VirtexE de la Xilinx. Configurabilitatea
reprezinta o parte importanta in controlul preciziei atat timp cat putem
controla totul in cadrul unui data-path. Toata aceasta munca a fost
efectuata utilizand dispozitive FPGA de un anumit tip
care au reprezentat tehnologia urmarita pentru implementarea finala. Justificarea utilizarii FPGA-urilor ca tehnologie urmarita in
aceasta cercetare vine din necesitatile industriale. Munca a fost
condusa dupa necesitati, avand obiectivul de a obtine
module de procesare a datelor care sa poata fi utilizate in data-path-urile
hardware, care sa poata genera semnale video decomprimate la o calitate de tip
studio. Produsele comerciale de succes in aceasta categorie nu se produc in
cantitati mari, iar de cand cu implementarea
algoritmilor bazati pe DSP-uri, durata lor de viata este relativ scurta ca si
cum ar fi inlocuiti cu algoritmi care sunt totusi alcatuiti din cateva module
functionale de baza, adesea necesare. Conceptele prezentate
aici ar putea fi utilizate in cadrul unui generator de module cu unitati in
virgula mobila, care ar reprezenta o completare la documentatiile exintente
privind generatoarele de module. In mod clar
conceptele amintite sunt aplicabile unei varietati de FPGA-uri. In continuare, documentatia prezinta doua tehnici inovative pentru
reducerea complexitatii si imbunatatirea performantelor implementarii hardware
utilizand formate in virgula mobila in cadrul FPGA-urilor.
Tehnica propusa
consta in:
·
utilizarea unui format configurabil in virgula mobila,
cu un bit-width redus, pentru a modifica structura de tip data-path la
cerintele algoritmului,
·
utilizarea clasicei inversari
si multiplicari asemanatoare impartirii, dar cu optimizari esentiale care sunt
posibile datorita utilizarii reprezentarii in virgula mobila pentru codarea
inversei.
2.UNITATEA
IN VIRGULA MOBILA
In general, o reprentare in virgula mobila permite,
pentru un numar fix de biti, reprezentarea unui
interval mai mare de valori pe un numar usor mai mic de biti. Acest lucru justifica utilizarea ei in aceasta aplicatie deoarece
se doreste limitarea numarului de biti utilizati pentru reprezentarea
intervalului de valori dorit.
IEEE 754 Standard [1] intermediaza cu reprezentarea in
virgula mobila si propune urmatorul tip de date pentru o valoare de precizie
simpla:
(-1)S x
1 . M x 2 E -127 ( 1
)
·
S : bitul de semn,
·
M : mantisa, codata de 23 de biti,
·
E : exponentul, codat de
8 biti.
In aceasta
reprezentare, mantisa este tot timpul normalizata, iar
cel mai semnificant bit al sau este intotdeauna 1. De aceea MSB-ul nu este direct codat in M, dar este implicat in reprentare
(1.M). Unul din avantajele majore urmaririi acestei reprezentari standard il constituie suportul sau in majoritatea procesoarelor in
virgula mobila si compilatoarele limbajelor de nivel inalt. Acest lucru este util pentru portabilitate.
De exemplu, procesorul SPARC [10] are o unitate in
virgula mobila care executa operatii asupra numerelor in simpla sau dubla
precizie. Unitatea in virgula mobila POWER2 de la IBM [6] a fost special
construita pentru a limita piedicile si a imbunatati
transferul de informatii. O comparatie detaliata cu unitatea POWER2 este dificila atat timp cat necesitatile hardware nu sunt
specificate in referinta. Totusi solutia propusa pare dificil de implementat. O
unitate in virgula mobila CMOS [3] implementand adunarea, scaderea si
inmultirea necesita un cip intreg de 330000 de
tranzistoare. Complexitatea este greu de tolerat in
data-path-uri ce necesita sute de operatii pe fiecare ciclu de ceas si unde
terminarea multor astfel de operatii necesita o reprezentare in virgula mobila.
Obiectivul acestei documentatii nu este
acela de a concura cu unitatile in virgula mobila ale microprocesoarelor
moderne ci doar pentru a demonstra avantajele reprentarii dinamice ordonate a
unitatii in virgula mobila comparata cu cea statica iar in mod particular si
atunci cand sunt implementate in FPGA-uri. Pentru instanta,
mantisa de 23 de biti duce la o complexitate inalta in inmultiri si impartiri.
Acest lucru este uneori ineficient in procesarea
video, atunci cand obiectivul este acela de a produce la iesire o imagine de o
calitate de 8 biti, cunoscuta sub numele de calitate studio. Un
format desprins din standardul IEEE a fost propus [8]. El consta intr-o
reprezentare pe 16 biti, cu bit de semn, exponent de 6 biti si mantisa de 9
biti. Operatorii folositi sunt un pic mai putin complecsi
decat cel cerut de IEEE-ul standard. Totusi este
special facut pentru un procesor aritmetic si de aceea formatul nu este
configurabil si nu permite configuratii ale data-path-urilor. De cand intr-o
structura speciala optimizata dorim sa gestionam dimensiunile
fiecarei date, o reprezentare hard-coded nu indeplineste cerintele.
Totodata in [2], o reprezentare pe 32 de biti derivata
din IEEE este prezentata si utilizeaza un exponent in
baza 8, reprezentand un interval mai mare decat formatul standard IEEE. In
acelasi timp duce si la o crestere monotona a mantisei pentru ambele numere,
pozitive si negative facilitand comparatia. Totodata, obiectivul acestui studiu
este de a optimiza executia codului in cadrul unui
procesor standard propus, care este complet diferit fata de studiul acesta. In
aplicatiile lor (software pentru control automatizat), comparatia este operatorul cel mai folosit si de aceea scopul este
optimizarea. Algoritmii urmariti in studiu necesita inmultiri
si impartiri, dar nu si comparatii in virgula mobila.
Aceste consideratii ne ghideaza in
conceperea unui format configurabil in virgula mobila. Cu acest format, noi putem alege numarul de biti utilizati pentru a
coda mantisa si exponentul. Corespunzator cerintelor aplicatiei
reprezentatia aleasa nu are semn.
Numarul este codat dupa formula
urmatoare:
M x 2 +E ( 2 )
Exponentul poate avea semn sau nu,
depinde de nevoile aplicatiei. O diferenta in comparatie cu IEEE-ul
standard este acela ca mantisa nu este totdeauna
normalizata. O reprezentare normalizata este utila
pentru comparatii, dar nu ofera un avantaj clar pentru impartiri si inmultiri.
Exemplele urmatoare ne arata avantajele acestei
reprezentari pentru utilizarea in mod general si care pot fi adaptate usor in
functie de cerintele aplicatiei.
Se
da 0100010000000000 pentru a fi codat cu o mantisa de 8 biti.
Rezultatul este 10001000∙27. In acest caz mantisa este normalizata.
Pe de alta parte se da 0000000000100010 pentru a fi codat.
Rezultatul
cu o mantisa normalizata ar fi 10001000∙2-2.
Rezultatul cu
unitatea noastra de virgula mobila este
00100010∙20.
Cele
doua rezultate sunt desigur echivalente, dar cea de-a doua nu adauga artificial
zerouri mantisei, si se poate evita reprezentarea cu semn pentru codarea
exponentului.
Daca M este un intreg si E este pozitiv, unitatea noastra de
procesare codeaza intregi scalari (exponentul este pozitiv), utilizand notiunea
de virgula mobila. Totodata, daca E este un numar cu
semn, formatul propus poate reprezenta valori fractionale.
De exemplu:
dandu-se 000001000∙100101 pentru a fi codat cu o mantisa de 8 biti
(echivalent cu 1000100101∙2-6), obtinem 10001001∙2-2
(echivalent cu 1000∙1001∙2-6+4). Este de mentionat ca in
cadrul unei unitati hardware dedicate, -6 poate fi virtual si nu este implementat. Este pur si simplu o
varianta de cum interpreteaza designer-ul iesirea furnizata de hardware.
De aceea ecuatia 2 este o reprezentare generala a
unitatii in virgula mobila.
In
multe aplicatii de procesare semnal, majoriatea datelor de procesat sunt in
virgula fixa. Totodata, data furnizata la iesire este adesea
tot in virgula fixa. Acesta este cazul cu imaginea si
procesarea video.
De aceea, avem nevoie de module de conversie;
virgula fixa – virgula mobila, pentru a implementa
unitatile necesare in virgula mobila in cadrul DSP-urilor.
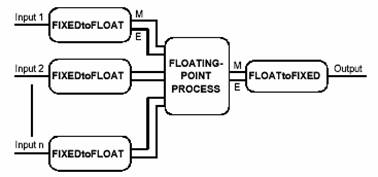
Figura
1 – Sistemul in virgula mobila
In cadrul acestei
documentatii, unitatea de conversie necesara se va
numi FIXEDtoFLOAT si FLOATtoFIXED.
2.1
MODULUL FIXEDtoFLOAT
2.1.1 Implementarea
Modulul
FIXEDtoFLOAT analizeaza datele ce urmeaza a fi
convertite intr-un format in virgula mobila, si corespunzator valorii obtinute,
realizeaza o schimbare inteligenta a bitilor semnificativi. Discutia urmatoare
presupune o mantisa de 8 biti si este usor generalizata
pentru alte dimensiuni.
Implicit, modulul
porneste determinand pozitia celui mai semnificativ bit ce
se afla pe 1, si selecteaza restul bitilor mantisei de pe acea baza. Exponentul
este numarul de biti dupa ce bitul cel mai putin
semnificativ a fost pastrat pentru mantisa.
De exemplu,
0|10001000|0010000|
M=10001000 E=7
Atunci cand nici un
bit mai semnificativ este pe 1, cei 8 biti semnificativi sunt pastrati ca
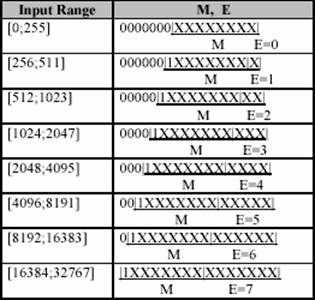
mantisa. Tabelul urmator ilustreaza acest algoritm in detaliu in cazul in care intrarea
de 15 biti este reprezentat cu o mantisa de 8 biti si
un exponent de 3 biti.
Tabelul
1 – Tabelul de conversie pentru un modul FIXEDtoFLOAT
2.1.2 Performante
Acest modul a fost
implementat in limbajul VHDL, sintetizat cu Synplify, incorporat pe un dispozitiv FPGA VirtexE XCV50E-6 de la Xilinx. In aceasta implementare, numarul de biti in mantisa si exponentul
sunt parametri generici.
In cazul in care o
intrare de 15 biti este reprezentata de o mantisa de 8 biti si un exponent de 3
biti, 35 de zone sunt necesare si presupunand cel mai rau caz de analiza a
timpului de operare, poate realiza operatiile la 105Mhz.
2.1
MODULUL FLOATtoFIXED
2.1.1 Implementarea
Acest modul ia datele in
virgula mobila si le returneaza intr-un format in virgula fixa. Desigur ca
realizeaza exact opusul operatiei modulului FIXEDtoFLOAT. Tabelul urmator
descrie in detaliu modificarea bitului de catre unitatea FLOATtoFIXED, atunci
cand o mantisa de 8 biti si un exponent de 3 biti returneaza o reprezentare de
15 biti in virgula fixa.
Tabelul
2 – Tabelul de conversie pentru un modul FLOATtoFIXED

Acest modul muta
bitii mantisei pe o pozitie alaturata si face
completarile cu zerourile necesare.
2.2.2 Performante
Acest modul este de asemenea configurabil pe parcursul pasului de
sintetizare pentru numarul de biti ai mantisei, exponent si iesire. Utilizand aceleasi
valori de biti 8, 3, si 15; dupa sintetizare, asezare, rotire si analiza a
timpului obtinem: o complexitate de 30 de zone si o frecventa de lucru de 85
Mhz cu un XCV50E-6 VirtexE (si 101 Mhz pentru
XCV50E-8).
2.3
Compararea performantelor cu implementari bazate pe FPGA-uri
Referitor la
complexitate, un multiplicator procesand o mantisa de 8 biti necesita 34 de
zone comparativ cu 290 necesare pentru un multiplicator de 23 biti in cadrul
unui format mobil Standard IEEE. Beneficiul obtinut vine din reducerea latimii
in biti; totodata, reprezentarea adoptata ne furnizeaza exact ce avem nevoie pentru aplicatia noastra.
Prin comparare, o
unitate in virgula mobila ce efectueaza adunare,
scadere si inmultire necesita un intreg XC4044XL Xilinx (380 CLB-uri,
echivalent cu 950 de zone Virtex) [7], iar 60% din acea complexitate este
necesara pentru implementarea inmultirii. Similar, unitatea
in virgula mobila CMOS amintita in referinta [3] utilizeaza 40% din spatiul sau
pentru implementarea inmultirii.
3.MODULUL
DE INVERSIE MATEMATICA
Reprezentarea in
virgula mobila este interesanta in cazuri particulare
cand sunt aplicate unui divizor, deoarece ii permite sa limiteze numarul de
biti, cat timp se pastreaza
O abordare clasica in
obtinerea unei impartiri este :
·
sa calculam inversa cu o reprezentare in virgula
mobila,
·
sa multiplicam aceasta inversa cu numaratorul
Aceasta metoda a
fost de asemenea utilizata in [8], dar autorii nu au folosit avantajele
reprezentarii in virgula mobila pentru codarea inversei si de aceea, latimea
datei multiplicarii urmatoare nu este oiptimizata.
Pentru cele mai
bune cunostinte, aceasta documentatie este prima ce propune
utilizarea reprezentarii in virgula mobila pentru efectuarea inversiei ca o
necesitate de limitare a complexitatii hardware. Aceasta metoda este foarte bine adaptata la ordinea dinamica obtinuta de
catre operatorul de impartire. Rezultatul obtinut este
in format in virgula mobila, care este inapoi transformat in format in virgula
fixa sau lasat in format in virgula mobila pentru eventualele operatii
urmatoare. Comparativ cu un algoritm de impartire
iterativ [5], aceasta metoda poate produce un rezultat in fiecare ciclu de ceas
la standardele cerute.
In
aceasta documentatie, ne concentram atentia asupra partii referitoare la
inversare. Un multiplicator clasic poate fi utilizat
pentru a finaliza impartirea.Exemplul urmator ne arata interesul utilizarii reprezentarii
in virgula mobila pentru codarea inversului:
Este dat un intreg pentru inversare. Inversul este
codat utilizand reprezentarile urmatoare:
2-1 2-2
2-3 2-4 2-5 2-6 2-7 2-8
….
Numarul de biti
utilizati depinde de acuratetea inversei cerute.
Inversa unui numar este calculata de:
Inv = Round(2x/x) (3)
·
Round, rotunjeste catre valoarea cea mai apropiata,
·
X : numarul de inversat
·
N : numarul de biti pentru codarea inversei
Functia de rotunjire este utilizata pentru
minimizarea erorii la ±1/2 LSB.
De exemplu, cu un numar de 6 biti pentru
inversare si N=13:
·
1/5 este codat 0011001100110,
·
1/62 este codat 0000010000100,
·
1/63 este codat
0000010000010.
Pentru obtinerea
unei bune acuratete, trebuie sa pastram o multime de
biti pentru codarea inversei. Abia al 11-lea bit face diferenta intre 1/62 si
1/63. Mai mult, chiar si cu 11 biti, precizia rezultatului este
de 6 biti, deoarece zerourile din fata nu cresc precizia ci indica doar latimea
rezultatului. Cu aceasta reprezentare, am obtine o precizie excelenta atunci
cand inversam numere mici, dar de precizie mica cand inversam numere mari. Mai mult, multiplicarea corespunzatoare inversiei ar
necesita operanzi mari.
De exemplu 1/63: 00000 10000010
Nr. de zerouri Partea semnificativa
din fata a inversei : 130
Cu virgula mobila,
precizia in biti este
Trebuie
mentionat ca inversorul poate trata cu ambele tipuri de date, in virgula mobila
si in virgula fixa. Pentru a procesa data in virgula mobila, trebuie sa ne asiguram ca inversam intreaga mantisa.Daca nu, trebuie
sa normalizam mantisa si sa pastram numarul cerut de MSB (pentru prevenirea
problemelor de precizie). Cand mantisa este
normalizata, trebuie sa scadem numarul zerourilor rezultatului din exponentul
de la intrare. Mai mult numaratorul poate fi un numar
fie in virgula mobila fie in virgula fixa.
3.1
Implementare
Designul este orientat catre implementarea FPGA. Deoarece numarul de
inversat in aplicatia noastra nu este foarte mare (6
biti), partea importanta a inversei este codata eficient intr-un ROM utilizat
ca un tabel de cautare, si numarul de zerouri sunt calculate utilizand logica.
Precizia ceruta presupune ca partea semnificanta a inversei sa
fie codata cu 8 biti. Numarul de spatii (zerouri), limitat la
5, necesita o codare pe 3 biti. Acesti parametri satisfac nevoile
aplicatiei noastre, dar inversul este in totalitate
configurabil pentru marimea de la intrare si rezultatul obtinut la iesire.
Trebuie notat ca daca dorim sa inversam numere mari,
devine mult mai interesant sa utilizam blocuri RAM decat cele LUT pentru
implementarea ROM-ului. Desigur, acest lucru depinde de
disponibilitatea resurselor in FPGA-urile utilizate.
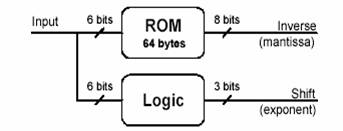
Figura
2 – Structura inversorului
Continutul ROM-ului este calculat pe parcursul pasului de sintetizare utilizand
formula (3) din care inlaturam cele mai semnificative zerouri. Calculul
numarului de zerouri este decodat din datele de
intrare utilizand tabelul urmator:
Tabelul
3 – Tabelul de conversie pentru calculul numarului de zerouri

3.2
Performante
Divizorul
primeste o intrare de 6 biti si furnizeaza o mantisa de iesire de 8 biti, adica
½ LSB. Se introduc doua etape in aceasta transformare.
A fost incorporat pe un FPGA VirtexE XCV50E-6 de la
Xilinx si analizat cu procedura descrisa anterior. Potrivit analizei timpilor,
frecventa de ceas poate fi de 145Mhz cat timp cererea
de spatiu este de numai 31 de zone.
Multiplicatorul este factorul ce limiteaza viteza.Acest modul de impartire
incape in 65 de zone. Acest lucru corespunde configuratiei de
baza a tabelului urmator.
Daca dorim sa imbunatatim performantele partii referitoare la
multiplicare, putem utiliza un multiplicator direct in procesul de
transformare. Cu trei pasi pentru aceasta multiplicare, frecventa de ceas poate
ajunge la 140Mhz, dar avem nevoie de mai multe zone
(un total de 80 pentur inversor si multiplicatorul procesului de transformare).
Acesta este raportat ca fiind cea mai rapida
configuratie in tabelul urmator.
Daca modulul de
impartire a fost implementat cu aritmetica in virgula fixa utilizand aceeasi
abordare, o precizie la iesire de 13 biti ar fi necesara in inversor si
multiplicatorul ar fi de 13 biti fata de 8, ceea este semnificativ mai mare si
mai lent.
Putem
compara implementarea noastra cu una in virgula fixa produsa de Xilinx,
utilizand programul CoreGenerator. Tabelul
urmator ne da rezultatele utilizand parametrii de mai sus cu acelasi dispozitiv
si aceleasi constrangeri de timp.
Tabelul
4 – Compararea performantelor
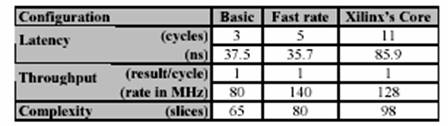
Implementarea
noastra in virgula mobila ofera o incetinire foarte scazuta. Totusi cand este necesar sa impartim numere mari, un astfel de
dispozitiv Core este mult mai eficient (mai mic, mai rapid), atat timp cat
valorile pentru dispozitivul nostru cresc exponential cu datele de la intrare.
Arhitectura noastra a fost destinata aplicatiilor ce
necesita o mantisa de pana la 10 biti.
4.CONCLUZIE
Reprezentarea in virgula
mobila pentru FPGA-uri bazate pe DSP-uri este adesea
considerata impracticabila. In contrariu, aceasta documentatie demonstreaza ca
o reprezentare in virgula mobila corespunzatoare inseamna o implementare
efectiva in data-path-uri DSP care mentin o acuratete buna la iesire pastrand
latimi de biti moderate. Utilizarea acestui format inovativ in virgula mobila este astfel un mod de a obtine o linie de mijloc intre
acuratete-complexitate-performanta.
5.BIBLIOGRAFIE
[1] ANSI/IEEE Std 754-1985 "IEEE Standard
for BinaryFloating-Point Arithmetic",1985.
[2] Connors, D.A., Yamada, Y. and Hwu, W-M.W.
"A Software-Oriented Floating-Point
Format for Enhancing
Automotive Control Systems", August 1999.
[3] Kelley, M.J. and Postiff, M.A. "A
CMOS Floating-pointUnit" 17th Annual Student
VLSI Design Contest,Experienced
Class Entry, 1997.
[4] Ligon III, W.B., McMillan, S., Monn, G.,
Stivers, F and Underwood, K.D. "A Re-
evaluation of
the Practicality ofFloating-Point Operations on FPGAs".
[5] Obermann, S.F. and Flynn, M.J.
"Division Algorithms andImplementations", IEEE
Trans. on Computers, Aug.1997,v.46, p.833-854.
[6] POWER2 Floating-point Unit: Architecture
and Implementation,
http://www.austin.ibm.com/tech/fpu.html.
[7] Sahim,
Reconfigurable Computing
Systems"MAPLD on Adaptative Computing, September
2000, vol.3.
[8] Shirazi, N., Walters, A. and Athanas, P.
"Quantitative Analysis of Floating-point
Arithmetic on FPGA Based Custom
Computing Machines" IEEE Symposium on
FPGAs for Custom
Computing Machines,
[9] Stamoulis,
Optimized
for FPGA Architectures"Lecture Notes in Computer Science, 1999,
v.1673, p.365-370.
[10] The SPARC Architecture,
http://www.cs.earlham.edu/~mutioke/cs63/sparc.htm#4.