1. Notiuni introductive
Circuitul de resicronizare este un circuit care poate optimiza intarzierea
unui circuit sincron prin deplasarea registrilor prin elemente de circuite
combinationale. Structura combinationala ramane neschimbata si comportamentul
observabil al circuitului este identic cu cel original.
In acest articol ne punem problema aplicarii tehnicilor de
resincronizare in circuitele FPGA (Field Programmable Gate Arrays).
Dispozitivele FPGA contin elemente de directionare prefabricate si configurabile,
care ne faciliteaza implementarea de diferite circuite. Totusi aceasta
interconectare contribuie decisiv la intarzierea totala a circuitului
implementat. Noi trebuie sa determinam daca exista castiguri semnificative
prin cuplarea resincronizarii si dispunerii astefel incat algoritmul de
resincronizare poate estima timpul de intarziere la directionare (Routing
Delays).
Design-urile implementate in FPGA sunt adesea dominate de
intarzierea asociata cu interconectarile lor configurabile. Aceasat se
datoreaza in principal faptului ca interconectarea (interconnect)
contine dispozitive ca tranzistoare de trecere, buffere tristate sau multiplexoare
la care se adauga conexiunile insasi.
Una dintre celemai puternici tehnici de optimizare a intarzierii
este resincronizarea secventiala (Sequential Retiming). Aceasta
tehnica deplaseaza registrii prin elemente de circuite combinationale
pentru a reduce lungimea cailor de sincronizare (timing-critical paths).
Tehnicile de optimizare a circuitului, ca resincronizarea, sunt aplicate
de obicei unei porti de nivel (gate-level netlist). Ne punem intrebarea
daca aceasta este solutia corecta din moment ce circuitul este dominat
de interconectarea flexibila a FPGA-ului.
In acest articol vom compara conventionala aplicare a resincronizarii
la o poarta de nivel cu un nou process de resincronizare aplicat dupa
dispunere. Aplicarea unei resincronizari secventiale dupa pasul de dispunere
ne ofera estimari corecte a timpilor de intarziere,dar impune noi provocari.
De exemplu poate sa necesite noi registri. Trebuie sa gasim un loc potrivit
pentru acesti registri aditionali din netlist, dar etapa de dispunere
sa terminat deja. Daca ar fi sa reluam etapa de dispunere, atunci am plati
un pret foarte mare in ceea ce priveste timpul de compilare. Pentru a
depasi aceste probleme introducem un nou algoritm de resincronizare impreuna
cu o facilitate de incrementare si dispunere a blocurilor. Acestnou alogoritm
de resincronizare incearca sa schimbe cat mai putin netlist-ul de dupa
dispunere. Daca acest algoritm de modificare minima a resincronizarii
hotaraste ca este necesar adaugarea de noi registri in netlist, atunci
unealta de incrementare si dispunere a blocurilor este folosita pentru
a gasi un loc pentru acesti registri de resincronizare. Acest proces poate
presupune mutarea sectiunilor logice non-critice pnetru a putea aseza
registrii de intarziere in locurile lor preferate.
In figurile de mai jos putem oberva diferentele dintre un
circuit normal si un circuit resincronizat.
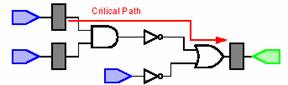
a)
Circuitul original
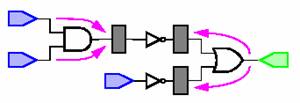
b) Circuitul resincronizat
![]() Fig.
1: Sincronizarea secventiala
Fig.
1: Sincronizarea secventiala
2. Resincronizarea (Retiming)
Resincronizarea secventiala este o puternica tehnica de optimizare
a circuitelor sincrone care au proprietatea ca flip-flop-ul poate fi mutat
de la iesirea portilor la intrarea lor si viceversa, fara a schimba comportamentul
circuitului. Folosind aceste deplasari se poate maximize viteza circuitului
si minimza aria de dispunere. Aceasta tehnica a fost introdusa in anii
1980 de catre Leiserson si Saxe. Ei au descris cativa algoritmi de resincronizare
secventiala pentru a minimiza intarzierea prin relocarea registrilor
in circuitele sincrone fara modificari ale functionalitatii lor.
Sa consideram circuitul din figura 1.a. Daca presupunem ca
intarzierea fiecarei porti este de o singura unitate de timp, atunci intarzierea
totala (critical path delay) este de 3 unitati de timp. Teoria resincronizarii
ne permite sa reducem intarzierea mutand punctele de flip-flop la intrarea
sau la iesirea portilor, asa cum este aratat in figura 1.b. Se observa
ca circuitul nu continue nici o cale cu o intarziere mai mare de o singura
unitate de timp. Singura modificare suferita de circuit a fost aceea de
relocare a registrilor.
2.1 Notatii si definitii
Algoritmii de resincronizare necesita o reprezentare unica a circuitelor
sincrone. Acestea sunt reprezentate de obicei sub forma unui graf orientat
G(V,E). V este multimea tuturor elementelor combinationale ale circuitului
, iar E este multimea arcelor directe euv; euv semnifica
legatura dintre celula de circuit combinational u si celula de
circuit combinational v, via zerosau mai multe register. Fiecare
arc direct are asociat o greuatate wuv, greutate care indica
numarulde registri dintre u si v. In figura 2 este ilustrat acest concept
de reprezentare.
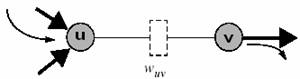 Fig.
2: Reprezentarea unui circuit de resincronizare
Fig.
2: Reprezentarea unui circuit de resincronizare
Un
circuit de resincronizare poate fi exprimat sub forma unui numar intreg,
numar care eticheteaza fiecare celula a circuitului. O eticheta r(v)
este asociat cu fiecare celula v. Aceasta eticheta indica numarul
de registri care sunt mutati de la intrarea celulei laiesirea ei. Astfel
numarul de registri pentru fiecare fir este dat de formula:
wr,uv
= wuv + r(u) - r(v)
(1)
Avand aceste definitii problema resincronizarii circuitelor sincrone poate
fi pusa in felul urmator: trebuie gasita o eticheta pentru fiecare celula
a circuitului astfel incat intarzierea celei mai lungi cai a circuitului
sa fie mai mica decat o perioda de ceas Φ. Aceasta problema
poate fi exprimata formal astfel:
·
Toate etichetel r(v) trebuia sa fie numere intregi
·
Dupa resincronizare toate greutatile trenuie sa fie pozitive.
·
Fie P calea dintre u si v. Fiecare cale din circuit cu intarzierea
D(P) mai mare decat Φ trebuie sa aiba cel putin un
singur registru pe toata lungimea ei.
D(P)> Φ - Wr,P≥1
D(P)> Φ - r(u)≥r(v)-WP+1
CantitateaWP reprezinta suma greutatilor arcelor de pe lungimile
lor.
Aceste conditii pot fi rezolvate de un algoritm de aflare a caii cele
mai scurte ca algoritmul Bellman-Ford.
Un concept fundamental folosit in resincronizare este acela ca numarul
registrilor din jurul unui ciclu din graful de resincronizare nu poate
fi schimbat prin aplicarea resincronizarii secventiale. Registrii pot
fi relocati in jurul ciclului, dar numarul lor nu poate fi schimbat.
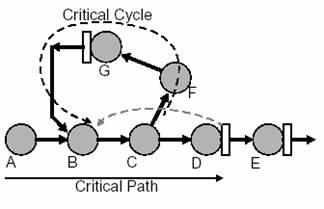 Fig.
3: Cicluri critice
Fig.
3: Cicluri critice
3.
Cicluri critice
Experimentele noastre cu resincronizarea au aratat ca solutiile de resincronizare
sunt adesea limitate de catre ciclurile critice din netlist. Aceasta situatie
este ilustrata in figura 3. Calea critica AB-C-D poate fi redusa mutand
registrul D si E inapoi. Totusi nu exista nici o posibilitate de a reduce
intarzierea in jurul ciclului B-C-F-G. Se poate deci ca acest ciclu sa
limiteze performanta resincronizarii. Scopul nostru este de a gasi o strategie
de dispunere.
Figura 4 ne arata un alt factor care limiteaza eficienta resincronizarii.
Un circuit resincronizat poate sa aiba mai multe cai apropiate de cele
critice. De exemplu calea critica A-B-C nu poate fi resincronizata deoarece
mutand registrul de la iesirea lui C inapoi, atunci calea apropiata ar
deveni critica. De asemenea, daca mecanismul de dispunere ar fi “inteles”
ca circuitul urmeaza a fi resincronizat, atunci el ar putea fi capabil
sa reduca intarzierea caii apropiate (D-E) de calea critica.
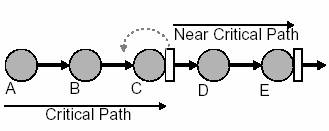 Fig. 4: Calea
critica
Fig. 4: Calea
critica
Pentru
ca dispozitivul de dispunere (placer) sa inteleaga solutiile de
resincronizare, este construet un graf din netlist-ul care este mapat.
El este denumit graful de rata a ciclului (cycle rate graph).
Figura 5. si figura 6. ne prezinta un graf de
resincronizare si un graf al ciclului (cycle rate graph) care corespunde
netlist-ului.
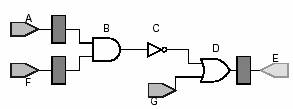 Fig.
5: Cycle rate netlist
Fig.
5: Cycle rate netlist
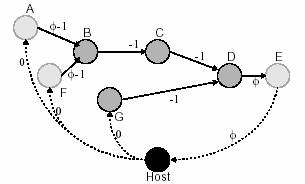
Fig.
6:Cycle rate graph
Fie Φ perioada de ceas dupa resincronizare. Un netlist de
resincronizare poate fi transformat intr-un cycle rate netlist
prin crearea unui graf cu aceleasi arce ca si netlist-ul de resincronizare.
Pentru fiecare euv din grafulde resincronzare vom crea o arca
echivalenta in graful de rata a ciclului (cycle rate). Totusi greutatea
unei arce din acest graf este wuv= Φ-d(v)-d(uv,),
unde d(v) este intarzierea nodului v, iar d(uv) este intarzierea arcei
de la u la v. Un nod special este adaugat la graf numit host. Acesta
este utilizat pentru a modela conexiunile cu sistemul extern pentru circuitul
considerat. Altfel algoritmul de resincronizare poate reduce calea critica
marind intarzierile de tip clock-to-output sau micsorand intarzierile
de tip clock-to-input. Arcele cu greutate 0 sunt adaugate de la host la
fiecare intrare primara. Arcele cu greutatea Φ sunt adugate
de la fiecare vertex primar la host-ul vertex. Fiecare vertex v
foloseste maxim –d(v) unitati de intarziere combinationale. Deoarece
numarul de registri din jurul ciclului ramane neschimbat, atunci suma
greutatilor din jurul orcarui cilcu C este Φ+Σcwuv-Σcd(v)-
Σcd(uv). Aceasta cantitate poate fi privita ca intarzierea totala
permisa de catre registri, minus intarzierea combinationala folosita.
Ea este denumita delay-toregister ratio (DDR) pentru ciclu. Viteza
de operare a circuitului este limitata de cel mai mare DDR pentru orice
ciclu din circuit.
Observati ca toate caile de la intrarile primare la iesirile primare participa
la ciclu din cauza conexiunii la vertexul host.
Pana acum am studiat cicluri singulare si am descoperit DDR-ul care limiteaza
valoarea lui Φ . Pentru a descoperi maximul DDR (MDR)
din graful cycle-rate, ne vom referi la gasirea unei valori minime
pentru Φ , care sa nu determine obtinerea unei valori negative
in graf. De exemplu in figura 6 o valoare de 0,5 pentru Φ ar
determina ciclul A-B-C-D-E-Host sa aiba o valoare negativa. 3*0,5-3=
-1,5. O tehnica simpla de gasire a valorilor negative a greutatilor este
de a rula un algoritm Bellman-Ford pe graf. Daca solutia nu este convergenta,
atunci in graf este prezenta o valoare negativa. Tehnica descrisa mai
sus ne permite sa gasim ciclurile care limiteaza perioadele de ceas. Pentru
a o aplica algoritmului de dispunere, vom defini conceptual de stagnare
de ciclu (cycle-slack). Pentru valoarea Φ gasita prin
procedeul de mai sus, cycleslack –ul unei conexiuni este maximul
intarzierii care care poate fi adaugata la conexiune fara a crea un ciclu
cu greutate negativa.
4.
Dispunerea minimala fara modificarea resincronizarii
Odata ce dispunerea este completa, urmatorul pas este acela al mutarii
registrilor pentru a resincroniza efectiv circuitul. Pentru o perioada
de ceas data, diferite secvente de mutari de registri ar pueta sa atinga
perioada de ceas. In aceasta sectiune articolului nostru vom prezenta
tehnici de determinare a secventelor de mutare a registrilor, secvente
care sa modifice cat mai putin netlist-ul post-dispunere. Acest pasva
face ca algoritmul de dispunere si incrementare a blocurilor (incremental
clustering and placement) sa fie ma usor de aplicat.
Prima provocare este de a modela registrii la iesirea blocurilor
logice FPGA in mod corect. Figura 7 ne arata o versiune simplificata a
unui bloc logic folosit destul de des in arhitecturile FPGA comerciale.
Blocul contine un table denumit lookup-table (LUT) cu un flip-flop
optional pentru a inregistra iesirea daca este necesar. Modelul luat in
considerare face presupunerea ca doar un singur semnal poate fi scos la
iesirea dintr-un bloc logic.
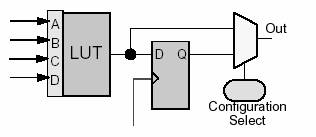 Fig.
7: Bloc logic FPGA
Fig.
7: Bloc logic FPGA
Figura 8 ne prezinta o schema de minimizare a duplicarii logice din timpul
resincronizarii. Figura 8.a arata nodurile extra adaugate in graful de
resincronizare pentru a modela blocul logic. Mai intai este adaugat un
singur nod la fiecare fanout de la iesirea din LUT. In figura
aceste noduri sunt notate F1i
si F2i. Un nod sursa
SRCi si un nod de tip sink SNKi sunt adaugate
pentru fiecare LUT. Fire sunt adugate de la SRCi la fiecare
nod fanout, si de la fiecare fanout la SNKi. Mai este
adaugata o conexiune virtuala de la SRCi la SNKi.
Putem afirma acum ca minimizand numarul de registri de pe firele virtuale,
minimizam si cantitatea de duplicare logica. Sa luam figura 8.b in considerare.
In acest caz mutam doar un singur registru inainte de la fanout la LUTi.
Exista acum doar un singur registru pe conexiunea virtuala de la SRCi
la SNKi. Acest lucru este posibil doar datorita mutarii registrului
de la fanin-ul SRCi. In figura 8.c ambele registre sunt
muate catre fanout. Observati acum ca exista tot un singur registru pe
conexiunea virtuala. Totusi el poate fi eliminat prim mutarea registrilor
de la fanin-ii SNKi-ului catre iesirea sa. Astfel minimizand
numarul registrilor de pe conexiunea virtuala avem un cost correct fara
a fi nevoie de o duplicare logica.
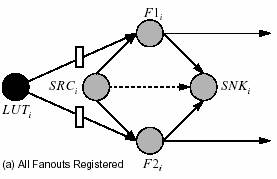
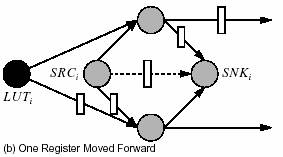
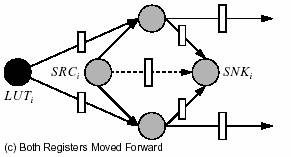 Fig.
8: Costul duplicarii logice
Fig.
8: Costul duplicarii logice
5.
Dispunerea si incrementarea blocurilor (incremental clustering and
placement - ICP)
Algoritmul ICP este folosit de fiecare data cand algoritmul de dispunere
minimala decide ca trebuie sa adauge registri suplimentari in netlist.
Acesti registri trebuie sa fie plasati undeva in FPGA. In mod ideal acesti
registri ar putea fi plasati pe zonele ramase neutilizate de pe chip.
Dar acesti registri de resincronizare sunt dispusi in locatii aleatoare
in netlist si algoritmul de dispunere incearca sa “impacheteze” logic
in mici zone pentru a minimiza intarzierea si lungimea firelor. De aceea
algoritmul ICP trebuie sa incerce sa creeze spatiu pentru registrii noi
inserati prin mutarea locatiilor fara intarziere sau a zonelor ce contin
fire critice.Elementele logice sunt organizate de obicei in grupuri sau
clustere. Figura 9 ne prezinta un model simplu de cluster FPGA.
Fiecare cluster contine NLUT elemete logice, NINPUT
linii de intrare, NClock intrari de ceas si NReset
intrari de tip set/reset asincrone. In literatura academica, de
obicei NLUT = 4, NINPUT =10 si NClock=NReset=1.
Aceste constrangeri semnifica faptul ca chiar daca exista destul spatiu
liber in FPGA,noi trebuie sa verificam daca avem destule linii de intrare,
ceas si reset disponibile. Ideea de baza din spatele algoritmului ICP
este de a-i plasa pe acesti registri in zonele lor preferate chiar daca
astfel sunt incalcate constrangerile de arhitectura.
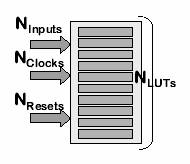 Fig.
9: Model de cluster FPGA
Fig.
9: Model de cluster FPGA
Algoritmul ICP are la baza o tehnica iterativa care muta celulele logice
in incercarea de a minimiza functia de cost. Aceasta functie de cost presupune:
· Cluster Legality Cost – fiecare cluster este penalizat daca contine o configuratie ilegala. Costul este proportional cu ilegalitatea.
· Timing Cost – costul de sincronizare eset folosit pentru a se asigura ca zone critice ale partii logice nu sunt mutate in locuri care ar mari in mod drastic intarzierea pe calea critica.
· Wirelength Cost – estimarea lungimii firelor este folosita pentru a se asigura ca circuitul este usor directionabil dupa ce are loc mutarea elementelor logice.
5.1 Cluster Legality Cost
Exista un cost al legalitatii clusterului asociat fiecarui cluster Ci, cost calculat astfel:
ClusteCost(Ci)= KLi*overuse(Ci,NLUT)+
KIi*overuse(Ci,NINPUT)+
KRi*overuse(Ci,NReset)+
KCi*overuse(Ci,NClock)
, unde overuse(Ci,NLUT) reprezinta numarulde extra LUT-uri continute de configuratia de cluster Ci, functia overuse este definite similar si pentru intrari, ceas si reset. Coeficientii KL, KI, KR si KC specifica importanta fiecarei overuse.
6.2 Timing Cost
Una din componentele costului de sincronizare este bazata pe costul utilizat de VPR. Acest cost este dat de relatia urmatoare:
TcostVPR=Σccrit(c)*delay(c)
Aceasta functie incurajeaza conexiunile critice sa reduca intarzierea si in acelasi timp permitand conexiunilor non-critice sa optimizeze lungimea firelor. Algoritmul ICP nu este definit pentru a optimiza intarzierea pe calea critica, ci mai degraba pentru prezerva intarzierea prin mutarea sectiunilor non-critice cat mai putin. O functie de cost “agresiva” ar putea sa determine transformarea sectiunilor non-critice in sectiuni critice. De aceea este introdus un cost de damping pentru a preveni prea multe mutari:
TcostDAMP=Σcmax(delay(c)-maxdelay(c),0)
maxdelay(C)=delay(c)+α*slack(c)
Valoarea lui maxdelay(c) este actualizata de fiecare data cand o analiza a sincronizarii este efectuata. Scopul functiei maxdelay este de a controla expansiunea intarzierii unei conexiuni date.
6.3 Wirelength Cost
Figura 10 ne prezinta o descriere de nivel inalt a modului cum este
monitorizata lungimea firului.
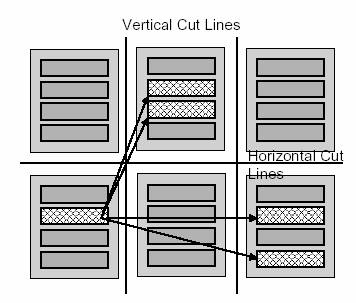 Fig.
10: Estimarea logica a congestionarii
Fig.
10: Estimarea logica a congestionarii
Liniile
orizontale si verticale de taiere sunt plasate in fiecare canal orizontal
si vertical al FPGA. Intretaierea acestor linii este contorizata la fiecare
mutare.
6.4 Propuneri de mutare
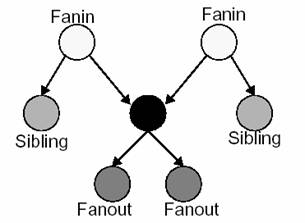 Fig.
11: Relatiile intre fanin, fanout si sibling
Fig.
11: Relatiile intre fanin, fanout si sibling
La fiecare iteratie a algoritmului ICP este ales un candidat dintre elementele logice LUTi pentru a fi mutat. Exista mai multe tipuri de mutari:
· Mutare-la-Fanin – se incearca mutarea lui LUIi laun cluster care contine un fanin al LUTi.
· Mutare-la-Fanout – se incearca mutarea lui LUIi laun cluster care contine un fanout al LUTi.
· Mutare-la-Sibling – figura 11 ne prezinta relatiile dintre LUTi . Se alese un sibling si se incearca muatrea lui la un cluster care contine un sibling.
· Mutare-la-Spatiu – se incearca mutarea in orice spatiu liber din FPGA.
·
Mutare-in-Directia-Vectorului-Critic – vectorul critic al
LUTi este aratat in figura 12. Directia vectorului critic este
aflata prin sumarea directiilor tuturor conexiunilor critice atasate la
LUTi . O incercare este efectuata de a se muat la un cluster
aleatoriu ales de-a lungul vectorului critic. Aceasta mutare ajuta la
corectarea oricarei greseli cand unele cai non-critice devin critice din
urma unor iteratii anterioare.
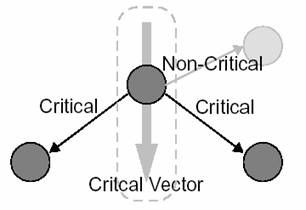 Fig.
12:Vectorul critic
Fig.
12:Vectorul critic
6.5 Algoritmul ICP
Algoritmul ICP este:
procICP
begin
while there is overuse remaining
choose any LUTi from an overused cluster;
select random move-type;
evaluate change in cost ΔC;
ifΔC < 0 then
accept move;
end if.
every K iterations do
run TA update crit(c) and maxdelay(c).
call UpdateOveruseCoefs;
end.
if loopIterations > Threshold then
return NO-FIT;
end if.
end loop.
end ICP.
Functiile de cost si propunerile de mutare au fost discutate mai sus.
Algoritmul ICP allege acele LUT-uri care sunt componente de clustere ilegale
si incearca sa le mute pentru imbunatati functia de cost. Observati ca
TA (Timing Analysis) eset efectuata la fiecare K iteratii. Acest
apel de functie actualizeaza maxdelay si valorile critice ale conexiunii.
Valoarea lui K este actualizata in functie de cantitatea de overuse
ramasa.
Doar mutarile care imbunatatesc functia de cost sunt acceptate. De aceea
algoritmul nostru este de tip greedy. Dezavantajul acestui algoritm
este acela ca el s-ar putea bloca in configuratii in care nu se pot gasi
mutari care sa scada costul curent. Pentru a combate aceasta problema
functia UpdateOveruseCoefs este apelata la fiecare K iteratii.
Ea mareste coeficientii de overuse pentru fiecare cluster care este ilegal.
procUpdateOveruseCoefs
begin
foreach overused cluster Ci do
KLi = KLi + overuse(Ci;NLUTs);
KIi = KIi + overuse(Ci;NInput);
KRi = KRi + overuse(Ci;NReset);
KCi = KCi + overuse(Ci;NClock);
end loop.
end UpdateOveruseCoefs
7. Concluzii
In acest articol am aratat care sunt castigurile de viteza care pot fi obtinute prin integrarea unor algoritmi deresincronizare si dispunere pentru FPGA in comparative cu resincronizarea lanivel de LUT.
8. Referinte
1. Altera. Altera 2000 Databook.
http://www.altera.com/html/literature/lds.html.
2. V. Betz, J. Rose, and A. Marquardt. Architecture and CAD for Deep-Submicron FPGAs. Kluwer Academic Publishers, 1999.
3. C. E. Cheng. RISA: Accurate and Efficient Placement Routability Modeling. In ICCAD 1994, 1994.
4. B. Cherkassky and A. V. Goldberg. Negative cycle detection algorithms
5. J. Cong and Y. Ding. FlowMap: An optimal technology mapping algorithm for delay optimization in lookup-table based FPGA designs. IEEE Transactions on CAD,1994.
6. J. Cong and S.K. Lim. Physical Planning with Retiming. Proc. IEEE International Conference on Computer Aided Design, 2000.
7. C. Leiserson, F. Rose, and J. Saxe. Optimizing synchronous circuitry. Journal of VLSI and Computer Systems, 1983.
8. C. Leiserson and J. Saxe. Retiming synchronous circuitry. Algorithmica, 1991.
9. N. Maheshwari and S. S. Sapatnekar. Efficient retiming of large circuits. IEEE Transactions on VLSI Systems, 1998.
10. L. McMurchie and C. Ebeling. PathFinder: A negotiation-based performance- driven router for FPGAs, 1995.
11. P. Pan. Continuous Retiming: Algorithms and Applications. International Conference on Computer Design, 1997.
12. P. Pan, A.K. Karandikar, and C.L. Liu. Optimal Clock Period Clustering for Sequential Circuits with Retiming. Transactions on Computer-Aided Design,
1998.
13. Xilinx. Xilinx 2000 Databook.
http://www.xilinx.com/partinfo/databook.htm.